之前在这我们已经讨论过快排、归并等排序方法,这些方法都具有一个特点:各元素间顺序依赖于比较,所以这些算法都被称为比较排序,对于这类方法,最优的下界为O(n lgn)。然而我们在这讨论为三种线性时间复杂度的排序方法:计数排序(Counting Sort)、基数排序(Radix Sort)和桶排序(Bucket Sort)。
计数排序
计数排序的基本思想为确定每个元素小于它的数量,就可以确定这个元素在排序完的列表中所处的位置。 计数排序要求输入的N个元素都必须是0到K的一个整数,当K=O(n)时,排序运行时间为O(n)。
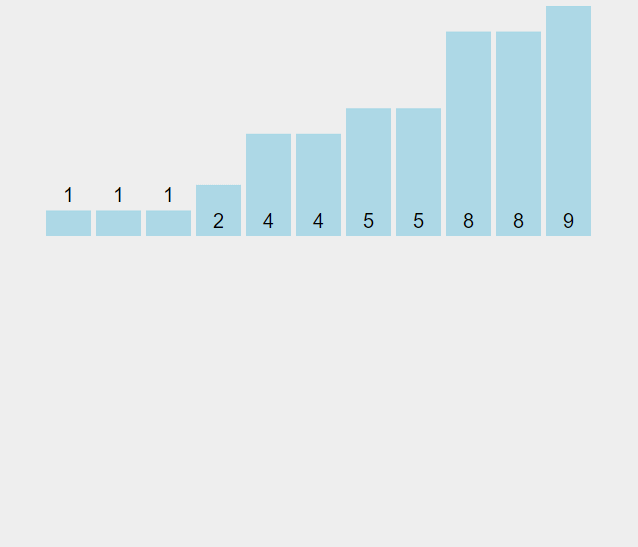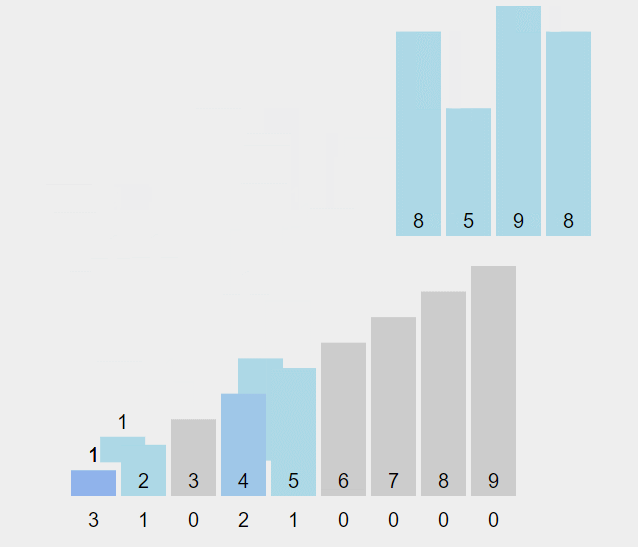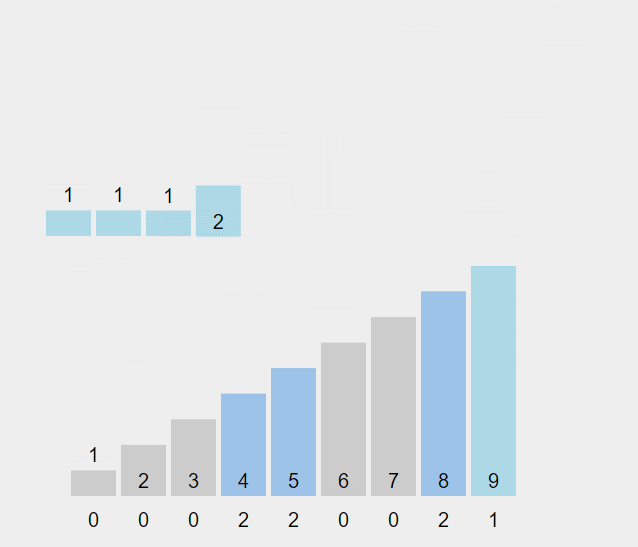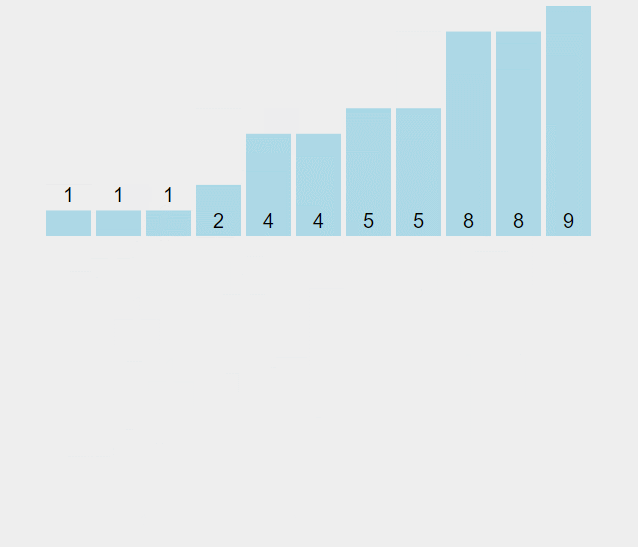
这里arr是我们需要排序的数组,max记录了最大的数据,tmp用来不同数据的数量,ans为存放输出的数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void counting_sort(vector<int>& arr, const int max) {
int *tmp = new int[max];
for (int i = 0; i < max; i++) tmp[i] = 0; //初始化tmp
for (int i = 0; i < arr.size(); i++) tmp[arr[i]]++; //此时tmp[i]即为i的数量
for (int i = 1; i < max; i++) tmp[i] += tmp[i - 1];
int *ans = new int[arr.size()];
for (int i = arr.size() - 1; i >= 0; i--) {
ans[tmp[arr[i]] - 1] = arr[i];
tmp[arr[i]]--;
} //生成结果
for (int i = 0; i < arr.size(); i++) {
arr[i] = ans[i];
} //拷贝回原数组
delete tmp;
delete ans;
}
基数排序
基数排序的基本思想为先将末位相同的放在一起,再依次排列产生一个具有新顺序的数组,再依次对十位、百位直至最高位做相同操作。

其中arr为要排序的数组,d为最高位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void radix_sort(vector<int>& arr,int d)
{
for (int i = 1; i <= d; i++) Rsort(arr, i); //依次对每一位排序
}
void Rsort(vector<int> &arr, int i) {
vector<vector<int>> vec;
for (int i = 0; i < 10; i++) {
vector<int> tmp;
vec.push_back(tmp);
}
int flag = pow(10, i);
for (int i = 0; i < arr.size(); i++) {
vec[(arr[i] % flag) / (flag / 10)].push_back(arr[i]); //放入对应的容器
}
int k = 0;
for (int i = 0; i < vec.size(); i++) {
for (int j = 0; j < vec[i].size(); j++) {
arr[k++] = vec[i][j]; //产生新数组
}
}
}
桶排序
桶排序的基本思想为在数据范围内划分n个相同大小的桶,然后将每个输入放入对应的桶中。桶排序要求输入数据均匀分布,所以桶中数据通常不会很多,可以很方便进行排序,排序完成后,依次输出即是结果。
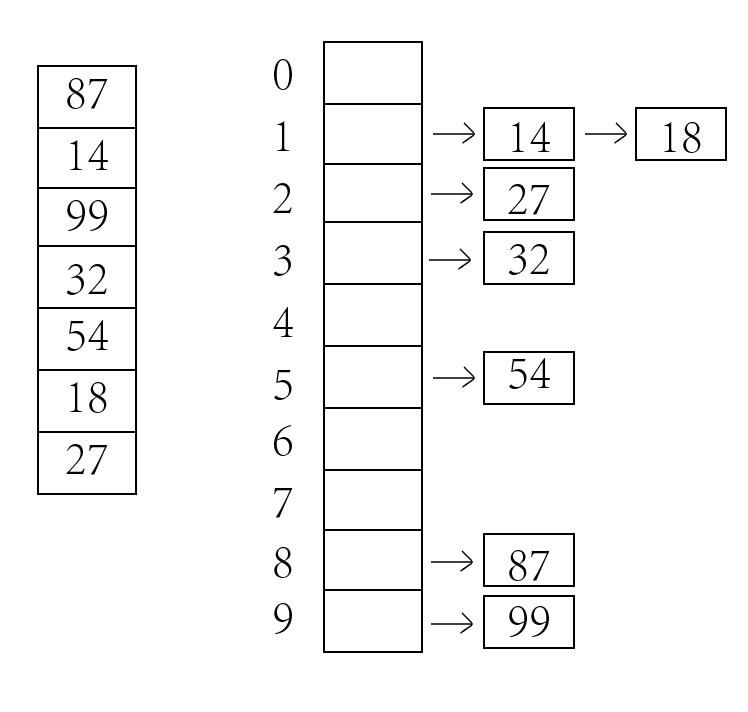
arr为要排序的数组,vec用来记录桶中元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void bucket_sort(vector<int>& arr) {
vector<vector<int>> vec;
for (int i = 0; i < 10; i++) {
vector<int> tmp;
vec.push_back(tmp);
} //初始化桶
for (int i = 0; i < arr.size(); i++) {
vec[arr[i] / 10].push_back(arr[i]);
} //放入桶中
for (int i = 0; i < vec.size(); i++) {
counting_sort(vec[i], 100);
} //对桶中元素排序,此处使用计数排序,也可使用其他排序方法
int k = 0;
for (int i = 0; i < vec.size(); i++) {
for (int j = 0; j < vec[i].size(); j++) {
arr[k++] = vec[i][j];
}
} //将结果输出至原数组
}
图片和gif根据 visualgo.net 制作